افترضت نظرية المنفعة الحدية أن المنفعة يمكن قياسها بوحدات تسمي “وحدات منفعة”، ولكن ظهرت آراء تشير إلى استحالة قياس المنفعة بوحدات كمية، وقيل إن نظرية طلب المستهلك ترتكز على فرض بعيد جداً عن الواقع. لذا ظهرت فكرة أخرى وهي منحنيات السواء تنادي بانه ليس من الضروري أن ترتكز نظرية طلب المستهلك على افتراض أن المنفعة قابلة للقياس، وأنه يكفي أن نفترض أن المستهلك قادر على الاختيار بين مجموعات من السلع والخدمات التي يستهلكها على أساس الإشباع الذي يستمده من إحدى هذه المجموعات بالمقارنة مع مجموعة أخرى.
فالمستهلك يستطيع ترتيب مجموعات السلع ترتيب تصاعدي او تنازلي وفقاً لدرجة الاشباع التي يحصل عليها من كل مجموعة. ويستطيع أن يقول إن المجموعة أ أفضل من المجموعة ب، والمجموعة ب أفضل من المجموعة ج، وبالتالي المجموعة أ أفضل من المجموعة ج. ويقارن المستهلك بين مجموعتين، فيرى أنهما متساويتان في نظره، فسواء اختار المجموعة الأولي أو الثانية، سيحصل على نفس مستوى الإشباع.
ما هو علم الاقتصاد؟
علم الاقتصاد هو العلم الذي يدرس القواعد المنظمة للسلوك الاقتصادي من خلال استخدام الوسائل المادية و الموارد المحدودة لإشباع الحاجات الإنسانية المتعددة. وعلي ذلك فالمشكلة الاقتصادية تتمثل في كيفية إشباع الحاجات المتزايدة باستخدام الموارد المحدودة.
مقالة ذات صلة: علم الاقتصاد: تعريفه، أهميته، فروعه، مناهجه
تعريف منحنيات السواء
منحنى السواء Indifference Curve هو منحنى يوضح مجموعات مختلفة من سلعتين تحقق للمستهلك نفس المنفعة او الاشباع. ونظرًا لأن جميع المجموعات تعطي نفس القدر من الرضا، يفضلها المستهلك بالتساوي، من هنا جاء اسم منحنى السواء. ويوضح الجدول التالي مجموعات مختلفة من السلعتين س، ص يفترض أنها تحقق للمستهلك نفس مستوى الاشباع.
| المجموعات | وحدات س | وحدات ص |
| الأولي الثانية الثالثة الرابعة الخامسة | 1 2 3 4 5 | 12 8 5 3 2 |
ووفقاً للمجموعة الأولي، يستهلك الفرد (وحدة من س، و (12) وحدة من ص فيحصل على إشباع معين. فإذا استهلك الفرد (2) وحدة من س، و (8) وحدة من ص (المجموعة الثانية) فانه يحصل على نفس مستوى الإشباع الذي يحققه له استهلاك المجموعة الأولى. وهكذا تتساوى المجموعات من حيث المنفعة. فسيان للمستهلك أن يختار أي من المجموعات التي يوضحها الجدول. ويوضح الشكل التالي منحني السواء الممثل للمجموعات السابقة.
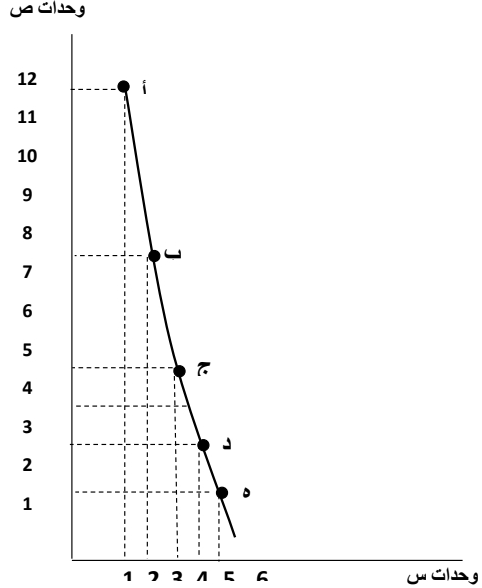
النقطة (أ) على منحني السواء تبين أن المستهلك يستهلك (12) وحدة من ص، ووحدة واحدة من س، في حين توضح النقطة (ب) انه يستهلك (8) وحدة من ص، و (2) وحدة من س. ونشير إلى أن جميع النقاط على منحني السواء تمثل مجموعات من السلعتين س، ص تحقق للمستهلك نفس مستوي الاشباع.
ويوضح الشكل التالي خريطة السواء الخاصة بالمستهلك (أ) حيث تتكون هذه الخريطة من مجموعة منحنيات سواء، كل منحني يحقق للمستهلك مستوي معين من الاشباع، ونشير إلى أن لكل مستهلك خريطة سواء خاصة به تعكس تفضيله للسلع، حيث تختلف خريطة السواء من مستهلك لآخر حسب درجة تفضيل كل مستهلك للسلع، أي حسب مستوي الاشباع الذي يحصل عليه المستهلك من المجموعات المختلفة من السلع.
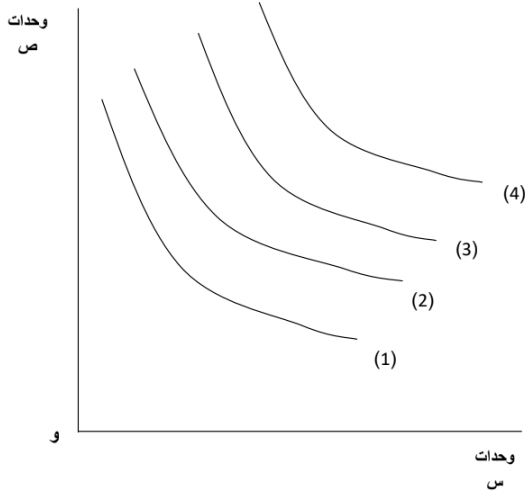
توضح خريطة السواء، في الشكل السابق، أربع مستويات للإشباع. فمنحني السواء رقم (1) يحقق للمستهلك مستوي معين من الاشباع. والمنحني (2) يحقق للمستهلك مستوي اشباع أكبر بالمقارنة بمنحني السواء رقم (1). وهكذا، كلما بعدنا عن نقطة الأصل واتجهنا لمنحني سواء أعلى، يزيد مستوي الإشباع الذي يحصل عليه المستهلك. فمن الطبيعي أن يفضل المستهلك مجموعات السلع التي تحتوي على كميات أكبر من السلعتين. وعليه فالمنحني رقم (4) يحقق للمستهلك أعلى درجة من الإشباع، يليه المنحني رقم (3) ثم (2)ثم (1).
معدل الاحلال الحدى
يقصد بمعدل الاحلال الحدي للسلعة “س” محل السلعة “ص” الكمية الواجب التخلي عنها من ص مقابل زيادة “س” بوحدة واحدة، وبحيث يظل المستهلك على نفس منحنى السواء، أي يظل يحقق نفس مستوى الإشباع ومع إضافة وحدات متساوية من “س” يتناقص معدل الإحلال الحدي كما يتضح من الجدول التالي:
| المجموعات | وحدات س | وحدات ص | معدل الاحلال الحدي |
| الأولي الثانية الثالثة الرابعة الخامسة | 1 2 3 4 5 | 12 8 5 3 2 | __ 4 3 2 1 |
توضح المجموعة الأولي أن المستهلك يستهلك وحدة واحدة من “س”، و(12) وحدة من “ص”. فإذا أراد المستهلك استهلاك وحدتين من”س”، فعليه أن يتخلى عن (4) وحدات من “ص” بحيث يحقق نفس مستوى الإشباع، أي يبقى على نفس منحنى السواء. ومعني ذلك أن منفعة الوحدة الإضافية من س تساوي منفعة (4) وحدات من “ص”. وإذا أراد المستهلك استهلاك 3 وحدات من “س”، فعليه أن يتخلى هذه المرة عن (3) وحدات من “ص”، أي عن كمية أقل من “ص”.
وهكذا في كل مرة تزيد الوحدات المستهلكة من”س” بوحدة واحدة، تقل الوحدات التي يتخلى عنها المستهلك من “ص”، حيث يظل يحقق نفس مستوى الاشباع. وتفسير ذلك أنه كلما كانت كمية “س” صغيره، ازدادت قيمة “س” مقومه بوحدات من “ص”، وكلما أحل المستهلك”س” محل “ص”، فإن كمية “س” تزيد وكمية “ص” تقل، وعليه تقل قيمة “س” مقومه بوحدات من “ص” أي تزيد أهمية الوحدات المتبقية من “ص”، في حين تقل أهمية الوحدة الإضافية من “س”، وعليه يكون المستهلك مستعداً للتخلي عن وحدات أقل فأقل من “ص” مقابل وحدة واحدة من “س”.
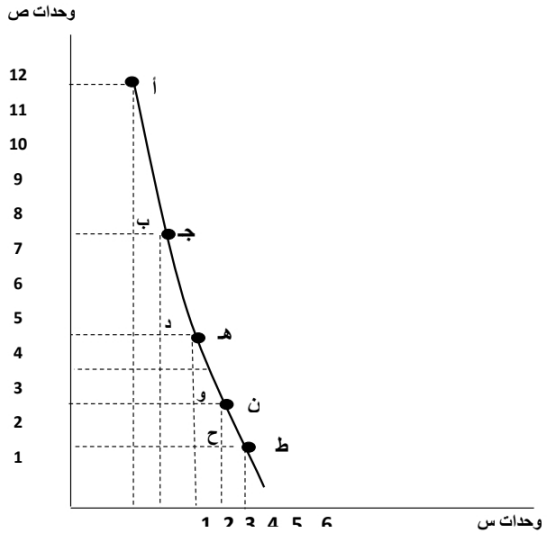
في الشكل السابق تخلي المستهلك عن (أ ب) من ص (4 وحدات) مقابل الحصول على (ب ج) من س (وحدة واحدة)، وبالتالي انتقل من النقطة (أ) إلى النقطة (ج) على نفس منحني السواء، ثم بعد ذلك تنازل من (ج د) من ص (3 وحدات) مقابل الحصول على (د هـ) من س (وحدة واحدة)، وانتقل المستهلك هذه المرة من النقطة (ج) إلى النقطة (هـ) على نفس منحني السواء. وهكذا، في كل مرة يتنازل المستهلك عن وحدات أقل فأقل من ص مقابل وحدة واحدة من س (هـ و < ج د < أ ب).
خصائص منحنيات السواء
تتسم منحنيات السواء بثلاث خصائص رئيسية هي:
أ. منحنيات السواء تنحدر من أعلى الي أسفل جهه اليمين
أي أنها سالبة الميل، ذلك أن زيادة الكمية المستهلكة من إحدى السلعتين لابد أن يصاحبها نقص الكمية المستهلكة من السلعة الأخرى. حتى يظل المستهلك على نفس منحنى السواء. ويبدو ذلك منطقياً للمحافظة على نفس مستوى الإشباع، إذ أن زيادة الكمية المستهلكة من كلتا السلعتين يترتب عليها زيادة مستوى الإشباع.
ب. منحنيات السواء محدبه تجاه نقطة الأصل
هذه الخاصية تعكس تناقص معدل الاحلال الحدي، بمعنى أننا إذا انتقلنا على طول منحنى السواء واحد من اليسار إلى اليمين فأننا نتخلى عن وحدات متناقصة من (ص) مقابل وحدة واحدة من (س)، (الشكل السابق).
ج. منحنيات السواء لا يمكن أن تتقاطع
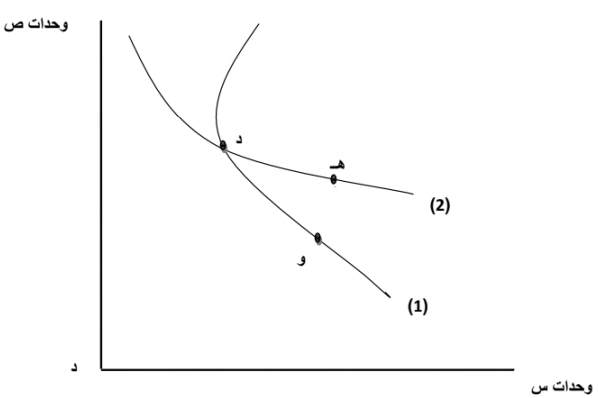
ويمكن إثبات ذلك بالنظر إلى الشكل التالي، ففي الشكل التالي، نفترض تقاطع منحني السواء رقم (1) مع منحنى السواء رقم (2). ويلاحظ ما يلي:
- النقطة د = النقطة و في الاشباع لأنهمايقعان على نفس منحني السواء (رقم 1).
- النقطة د = النقطة هـ في الاشباع لأنهمايقعان على نفس منحني السواء رقم (2).
- إذن النقطة هـ = النقطة و في الاشباع.
ولكن هذا غير صحيح، حيث أن النقطة هـ تقع على منحني سواء أعلي. وتعكس كميات من س، ص أكبر بالمقارنة بالنقطة و. أي أن كميات س، ص التي تمثلها النقطة هـ تحقق مستوي إشباع أكبر من الكميات التى تمثلها النقطة و. وعليه من المستحيل أن تتقاطع منحنيات السواء.
أهمية منحنيات السواء
منحنيات السواء هي أداة مهمة في علم الاقتصاد لتحليل تفضيلات المستهلك واتخاذ القرار. فيما يلي بعض الأسباب التي تجعل منحنيات السواء مهمة:
- تفضيلات المستهلك: تمثل منحنيات السواء تمثيلًا رسوميًا لتفضيلات الفرد على مجموعات مختلفة من السلع أو الخدمات. إنها تظهر المجموعات المختلفة للسلع التي توفر للمستهلك نفس المستوى من الرضا أو المنفعة. ومن خلال تحليل منحنيات السواء، يمكن للاقتصاديين اكتساب نظرة ثاقبة على تفضيلات المستهلك وفهم كيفية اتخاذ الأفراد خيارات في تخصيص مواردهم.
- تعظيم المنفعة: ترتبط منحنيات السواء ارتباطًا وثيقًا بمفهوم تعظيم المنفعة. ويهدف المستهلكون إلى زيادة رضاهم أو فائدتهم إلى أقصى حد نظرًا لقيود الميزانية وأسعار السلع. وتساعد منحنيات السواء في تحديد حزمة الاستهلاك الأمثل التي تزيد من المنفعة من خلال إظهار مجموعات السلع التي توفر أعلى مستوى من الرضا ضمن القيود المحددة.
- معدل الاحلال الحدى: توفر منحنيات السواء طريقة لقياس معدل الاحلال الحدى بين سلعتين. يمثل معدل الاحلال الحدى المعدل الذي يكون فيه المستهلك على استعداد للتخلي عن سلعة واحدة للحصول على وحدة إضافية من سلعة أخرى مع البقاء على نفس المستوى من الرضا. ويساعد فهم معدل الاحلال الحدى الاقتصاديين على تحليل كيفية تبادل المستهلكين بين السلع واتخاذ قرارات بشأن أنماط استهلاكهم.
- تغيرات الدخل والسعر: يمكن استخدام منحنيات السواء لتحليل آثار التغيرات في الدخل أو الأسعار على خيارات المستهلك. وعندما يتغير الدخل، سوف تتغير حزمة الاستهلاك الأمثل للمستهلك وفقًا لذلك. وبمقارنة منحنيات السواء القديمة والجديدة، يمكن للاقتصاديين تحديد التأثير على رفاهية المستهلك والتغيرات في كميات السلع المستهلكة.
- فائض المستهلك: ترتبط منحنيات السواء بمفهوم فائض المستهلك. ويقيس فائض المستهلك الفرق بين إجمالي المبلغ الذي يرغب المستهلكون في دفعه مقابل سلعة والمبلغ الإجمالي الذي يدفعونه بالفعل. ويمكن أن تساعد منحنيات السواء في تقدير فائض المستهلك من خلال تحديد الحد الأقصى للسعر الذي يرغب المستهلكون في دفعه مقابل كميات مختلفة من سلعة ما.
- تحليل السياسة: منحنيات السواء لها تطبيقات في تحليل السياسات الحكومية. ويمكن استخدامها لتقييم آثار تدخلات السياسة، مثل الضرائب أو الإعانات الحكومية، على رفاهية المستهلك. فمن خلال تحليل التغيرات في منحنيات السواء، يمكن للاقتصاديين تقييم تأثير تدابير السياسة على خيارات المستهلك والرفاهية الاجتماعية الشاملة.
مقالة ذات صلة: نظرية القيمة: ماهي، تطورها
توازن المستهلك
يكون المستهلك في حالة توازن إذا حقق أقصى إشباع ممكن في ظل دخله المحدود، وفي ظل الأسعار السائدة في السوق. بمعني آخر، يحقق المستهلك التوازن إذا استطاع أن يصل إلى أعلى منحنى سواء ممكن في ظل القيود السابق الإشارة إليها (الدخل والأسعار). ومن هنا يتضح أنه حتى يمكننا أن نتعرف على سلوك المستهلك الرشيد، فإن علينا أن نقوم بتمثيل هذين المتغيرين (الأسعار والدخل) بيانياً بأسلوب يبين لنا المدي الذي يمكن للمستهلك أن يتحرك فيه على خريطة السواء.
وحتى يمكننا أن نبين الطريقة التي تمثل بها هذين المتغيرين فإننا نسوق المثال التالي:
سنفترض أن دخل المستهلك =00ا دولار، وأنه ينفق كل هذا الدخل على شراء سلعتين: س، ص. وأن سعر الوحدة من س:10 دولار، وسعر الوحدة من ص = 5 دولار. فإذا قام المستهلك بإنفاق كل دخله على شراء السلعة س، دون أن يشتري شيئاً من ص، فإنه يحصل على 10 وحدات، والتى تعادل قيمة الدخل / ثمن الوحدة، وإذا أنفق كل دخله على شراء السلعة ص، دون أن يشتري شيئاً من س فإنه يحصل على 20 وحدة، والتى تعادل قيمة الدخل / ثمن الوحدة. وقد يقوم المستهلك بتوزيع دخله على شراء السلعتين، كما في الجدول التالي:
| وحدات س | وحدات ص |
| 10 | صفر |
| 9 | 2 |
| 8 | 4 |
| 7 | 6 |
| 6 | 8 |
| 5 | 10 |
| 4 | 12 |
| 3 | 14 |
| 2 | 16 |
| 1 | 18 |
| صفر | 20 |
فيستطيع المستهلك شراء 10 وحدات من س دون أن يشتري من ص، أو شراء 9 وحدات من س، ووحدتين من ص، أو 8 وحدات من س، 4 وحدات من ص.. وهكذا. ويمكن تمثيل الجدول السابق بيانيا من خلال ما يسمي بخط السعر حيث يبين هذا الخط المجموعات المختلفة من السلعتين التي يمكن للمستهلك شراءها في حدود دخله وفي ظل الأسعار السائدة لهاتين السلعتين في السوق.
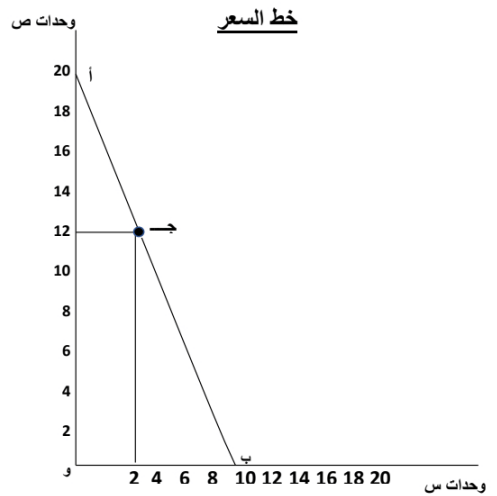
في الشكل السابق، نقيس على المحور الأفقي الكميات التي يمكن أن يشتريها المستهلك من السلعة س، وعلى المحور الرأسي الكميات التي يمكن أن يشتريها من ص. الخط أ ب يمثل خط الدخل. وتشير النقطة أ إلى أن المستهلك يشتري 20 وحدة من ص، وصفر وحدة من س٠ في حين تشير النقطة ب إلى أنه يشتري 10 وحدات من س٠ وصفر وحدة من ص. وتشير النقطة ج إلى أن المستهلك يشتري 12 وحدة من ص و4 وحدات من س.
وأي نقطة على خط السعر (أ ب) تبين وضعاً من الأوضاع التي يستطيع فيها المستهلك أن يوزع إنفاقه على السلعتين حسب أسعارهما السائدة في السوق. ولا يستطيع المستهلك أن يتعدى خط السعر، ذلك أن أي نقطة خارج هذا الخط تمثل وضعاً لا يمكن للمستهلك الوصول إليه بدخله المحدود. فهي تمثل كميات من س، ص يتطلب شراؤها عند مستوي من الدخل أعلى من ذلك الذي يمثله الخط أب. ولا يمكن أيضاً للمستهلك ان يتخذ وضعا تمثله نقطة أسفل خط السعر، إذ معنى ذلك أن المستهلك لا ينفق كل دخله.
وعليه فإن توازن المستهلك يتحقق عند نقطة ما على خط السعر، حيث جميع النقاط على هذا الخط يفترض فيها أن المستهلك ينفق كل دخله. كما أن هذه النقاط توضح مجموعات السلعتين س، ص التي يمكن شرائها في ظل الأسعار السائدة لهاتين السلعتين. وإذا كان توازن المستهلك أي تحقيقه لأقصي إشباع ممكن من إنفاق دخله المحدود على السلعتين س، ص يتحقق عند نقطة ما على خط السعر، فإنه لتحديد هذه النقطة يجب أن نضيف خريطة سواء هذا المستهلك إلى الشكل السابق. أي نجمع بين منحنيات السواء لمستهلك ما، وبين خط السعر لهذا المستهلك.
فلو أخذنا خريطة منحنيات السواء للمستهلك وأدمجنا في هذه الخريطة نفسها خط السعر لهذا المستهلك لظهر لنا الكميات التي يشتريها المستهلك من كل من السلعتين، والتي تحقق له أفضل توزيع لدخله، ويتضح ذلك في الشكل التالي.
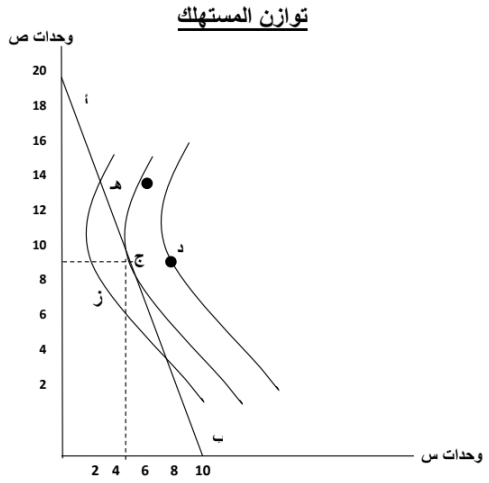
في الشكل السابق، يتحقق توازن المستهلك عندما يتماس خط السعر مع أحد منحنيات السواء، حيث يكون هذا المنحني هو أعلي منحني سواء يمكن للمستهلك الوصول إليه في ظل دخله المحدود، وأسعار السلع السائدة في السوق، أي في ظل القيوم المتمثلة بخط السعر.
وعند نقطة التماس ” ج ” يوزع المستهلك دخله بحيث يشتري 10 وحدة من ص، 5 وحدة من س. وأي نقطة أخرى غير النقطة “ج” لا تحقق التوازن للمستهلك. فالنقطة “د” واقعه أعلى خط السعر وهي تمثل كميات من السلعتين س، ص تحقق للمستهلك مستوي اشباع أكبر بالمقارنة بالنقطة ” ج “، حيث أن النقطة “د” تقع على منحني سواء أعلى، ومع ذلك لا يستطيع المستهلك شراء هذه المجموعة من السعلتين س، ص الممثلة بالنقطة “د”، حيث أنها تتطلب مستوى دخل أكبر.
والنقطة “ز” تقع أسفل خط السعر، وهي تمثل مستوى منخفض من الاشباع بالمقارنة بالنقطة “ج” حيث انها تقع على منحني سواء أدني، بالإضافة إلى أن المستهلك لا ينفق كل دخله عند هذه النقطة, والنقطتان “هـ”، “و” تقعان على خط السعر ومع ذلك لا تحققان التوازن للمستهلك، حيث أنهما تقعان على منحني سواء أدني من ذلك الذي تقع عليه النقطة “ج”، وعليها فهما يمثلان مستوي اشباع أقل بالمقارنة بالنقطة “ج”.
مما تقدم يتضح أن نقطة التماس بين خط السعر واحد منحنيات السواء هي النقطة التي يتحقق عندها توازن المستهلك. وعند هذه النقطة يتساوى ميل منحني السواء مع ميل خط السعر.
ولما كان: ميل خط السعر بالنسبة للمحور الأفقي = سعر الوحدة من س / سعر الوحدة من ص و ميل منحنى السواء بالنسبة للمحور الأفقي = الإحلال الحدي للسلعة س محل السلعة ص.
فإنه في حالة التوازن: معدل الاحلال الحدي للسلعة س محل السلعة ص = سعر الوحدة من س / سعر الوحدة من ص
مقالة ذات صلة: توازن السوق: ما هو، كيفية حسابه، العوامل التي تؤثر عليه
استخلاص منحنى الطلب لسلعة ما باستخدام منحنيات السواء
يوضح منحنى الطلب — كما وضحنا في مقالة سابقة— الكميات المطلوبة من سلعة ما عند الأسعار المختلفة. ويمكن اشتقاق منحني الطلب على السلعة س من خلال الاستعانة بفكرة توازن المستهلك. فالمستهلك — عند التوازن — يشتري 5 وحدات من س، وذلك بفرض أن سعر الوحدة من س(10) دولار. وعلى ذلك، حصلنا على نقطة على منحني طلب المستهلك على السلعة س، وهي النقطة التي يكون عندها سعر الوحدة من س 10 دولار، وكمية س 5 وحدات.
وللحصول على باقي نقاط منحنى الطلب على السلعة س، نفترض تغير سعر الوحدة من س، مع ثبات سعر ص، وثبات دخل المستهلك، لتري تأثير ذلك على توازن المستهلك وبالتالي على الكمية المشتراه من السلعة س. فنفترض أن سعر الوحدة من سن ارتفع من (10) دولار للوحدة إلى (20) دولار للوحدة. ويوضح الشكل التالي تأثير ذلك على توازن المستهلك.
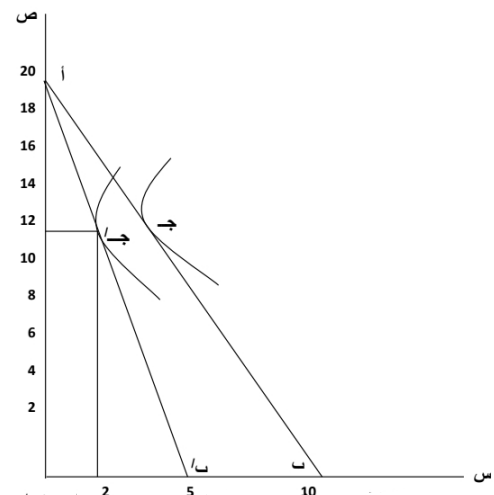
يوضح الشكل السابق أثر ارتفاع سعر “س” على توازن المستهلك، حيث ترتب على ارتفاع سعر س، مع ثبات سعر ص انتقال خط السعر من أ ب إلى أ بَ. فإذا أنفق المستهلك كل دخله على شراء ص يحصل على 20 وحدة. ولو أنفق كل دخله على شراء س يحصل على 5 وحدات. وقد يوزع دخله على شراء، ص. وهناك عدة مجموعات من السلعتين يوضحها خط السعر أ بَ.
ويتحقق توازن المستهلك على خط السعر أ بَ عند النقطة جَ، حيث يتماس هذا الخط مع أحد منحنيات السواء. وعند نقطة التوازن الجديدة (جَ) يشتري المستهلك (أ) وحدة من س. وبذلك نكون قد حصلنا على نقطة أخرى على منحنى الطلب على السلعة س، وهي النقطة التي يكون عندها سعر الوحدة من س 20 دولار، والكمية المطلوبة من س وحدة واحدة. وهكذا، بتغير سعر س، مع ثبات سعر ص ودخل المستهلك، ويمكن الحصول على عدة نقاط على منحني الطلب على السلعة س٠ وبتوصيل هذه النقطة نحصل على منحني الطلب على هذه السلعة كما هو موضح بالشكل التالي.
ويوضح الشكل التالي منحني الطلب على السلعة س المشتق من الأشكال السابقة. فعندما كان سعر الوحدة من س (10) دولار، كانت الكمية المطلوبة، (5) وحدات. وتم الحصول على هذه الكمية من النقطة (ج) والتي تمثل توازن المستهلك قبل تغير سعر السلعة س. وإذا ارتفع سعر الوحدة من س ليصبح (20) دولار للوحدة، تكون الكمية المطلوبة (2) وحدة. وتم الحصول على هذه الكمية المطلوبة (جَ) في الشكل السابق. والتي تمثل وضع توازن المستهلك بعد ارتفاع سعر السلعة س.
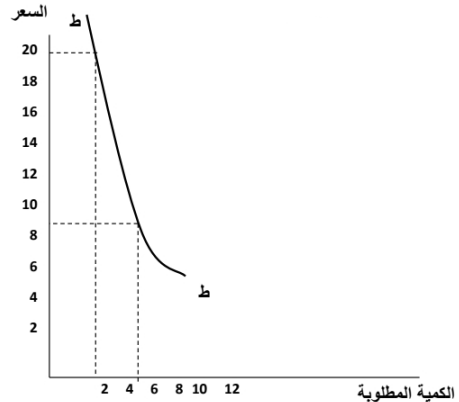
وهكذا يمكننا اشتقاق منحنيات طلب المستهلكين الأفراد باستخدام منحنيات السواء. وبجمع منحنيات طلب المستهلكين الأفراد جمعاً أفقياً — كما وضحنا في مقالة سابقة — نحصل على منحني طلب السوق.
فى النهاية آخر نقطة انت من ستضيفها فى التعليقات، شارك غيرك ولا تقرأ وترحل.